
|

|
|
Executive summary
This tool takes in a list of proteins or protein-interactions and searches for significantly enriched, short, linear motifs and ranks them by combining scores from over-representation, conservation, motif-like amino acids, overlap and motif-fit onto the surface of interacting three-dimensional structures (if available).
In more detail...
This tool integrates several previously developed tools from the Russell group. Given a set of sequences, a set of uniprot accessions/identfiers/gene-names or a set of interacting proteins, the method runs several tools. The results are integrated by Bayesian combination to give a ranked list of candidate motifs, with significance measures.
The methods used are:
- DiLiMOT, which detects over-represented motifs from a filtered set of input sequences
- PepSite, which computes the compatability between a peptide and a protein surface
- How well the motif instances are conserved across orthologues or close relatives
- A measure of how "motif-like" the motif is (i.e. based on how often particular amino acids are seen in known motifs)
- A measure of how motif-like the regions where the motifs are found - in terms of similar motifs found repeatedly
This is a big re-boot of earlier work, specifically DiLiMot and PepSite developed in the mid 2000s, with a lot of new ideas and improvements.
Even more detail...
 |
 |
 |
 |
Motif over-representation
The starting point of this pipeline is a search for any motifs that are significantly over-represented in a set of sequences. We use a version of the TEIRESIAS algorithm to find motifs within sequences that have first normally been filtered to remove regions unlikely to contain motifs, or regions that are already represented by homologous segments in the same set (more about this below). For the presence of a motif in a total of n out of M sequences we use a Binomial probability using a background probability of the motif occuring randomly in a set of similarly filtered sequences.
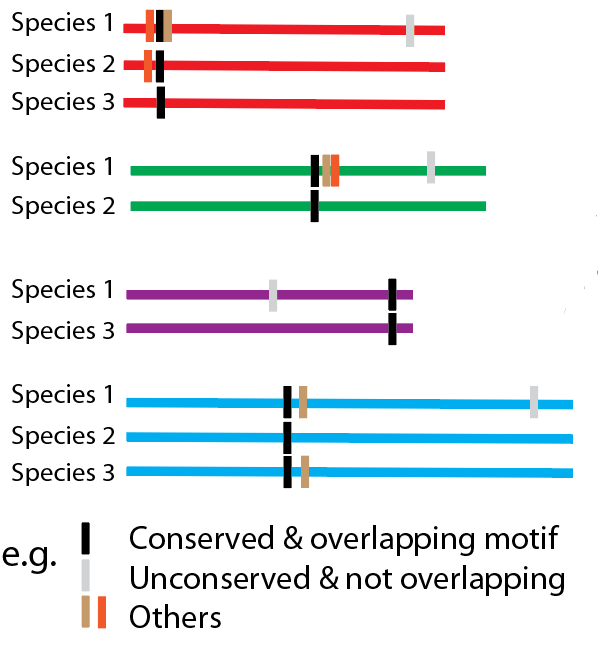
Conservation in orthologous sequences
We correct the above Bionomial probability by considering how well the motif is conserved within orthologous sequences for the approprate species group within the EggNOG database. Previously we simply multiplied these probabilities together (to get something we called Scons; see Neduva et al, 2005). However, this presumed that all instances of the motif across homologous species were independent, which is a wild over-estimate. We thus modified this by raising each species p-value to a power that captures how many effective independent observtaions there are. This measure is based on a rough idea of how orthogonal species are to each other. For example, seeing a motif in Mouse as well as Human does not improve the probability much, though seeing it in Yeast will improve confidence considerably (though this rarely happens).
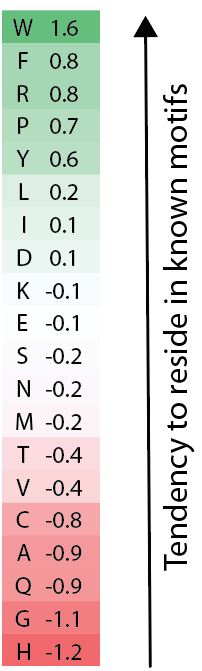
How much does the motif look like other motifs?
Certain amino acids are very common in the hundreds of known linear motifs. We capture this in a metric that is a sum of the log odds comparing how frequent each amino acid is in motif instances compared to other protein regions. Residues like Tryptophan (W), Arginine (R) or Proline (P) are very likely in contrast to residues like Alanine (A) or Glycine (G) which are rare in known motifs.
Motifs occuring as multiple variations around a theme
An observation we have made previously is that when a real motif is found (e.g. in a set of proteins sharing a common interaction partner), it tends not to be found as a single, discrete motif, but as a series of motifs with variations around a common core (e.g. SH3 motifs might be PxPxxP or PxxPxP around a core PxxP motif). We thus introduced a metric that counts how often motif instances for significant motifs overlap with those from other significant motifs.
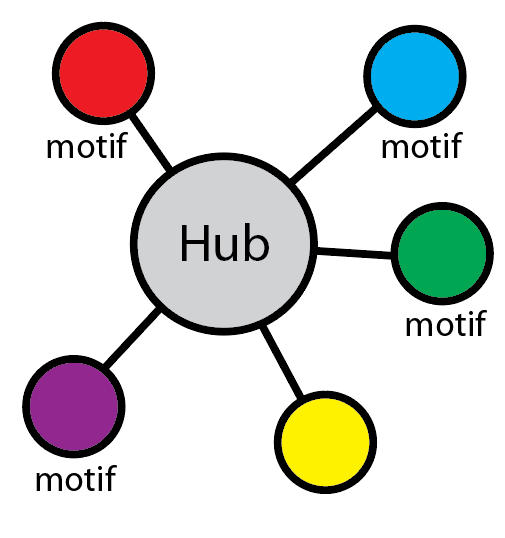
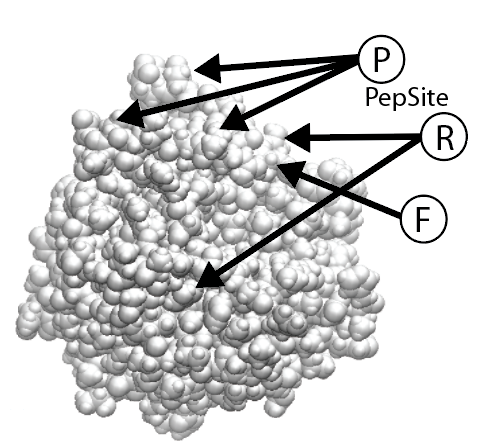
Fit to the surface of a hub protein (PepSite)
In most cases motifs interact with one or more specific partner proteins (which we call hubs or perpetrators). If a structure is available, then we make use of our program PepSite to see if any of the peptide instances found fit well onto any available structures for the hubs. By default, we only consider the top four structures sharing 70% or more sequence identiy with the hub protein (similarities detected using BLAST. It is possible to view the predicted binding sites by clicking on the relevant links.
Filtering sequences
Many parts of proteins are very unlikely to contain motifs. First, motifs tend to occur in non-globular, or un-structured or disordered parts of proteins, since this renders them more accessible to their binding partners (in contrast to parts that are buried in a structured domain). Moreover, it is well established that motifs are not descended from a common ancestor in the same way that protein-domains are. That is, we believe that motif instances appear spotaneously in protein sequence by convergent, instead of divergent, evolution. For this reason, it is important that no homology is present in the sequences before running the search. If they are present, then the over-representation becomes problematic as instances of putative will be appear that are the result of homology.
We have four means to remove regions unlikely to contain motifs:
- Sequence homology redundancy filtering: regions that are homologous (assessed by BLAST) to other regions already in the set
- Uniprot region filtering: Regions that are annotated in Uniprot to be regions not likely to contain motifs (specifically: STRAND, HELIX, TRANSMEM, SIGNAL, DISULFID, METAL or COILED)
- Ordered sequence (IUpred) filtering: Regions identified as globular using IUpred
- Structure domains filtering: Regions identified as globular by similarity to protein domains of known structure
Bayesian combination of scores
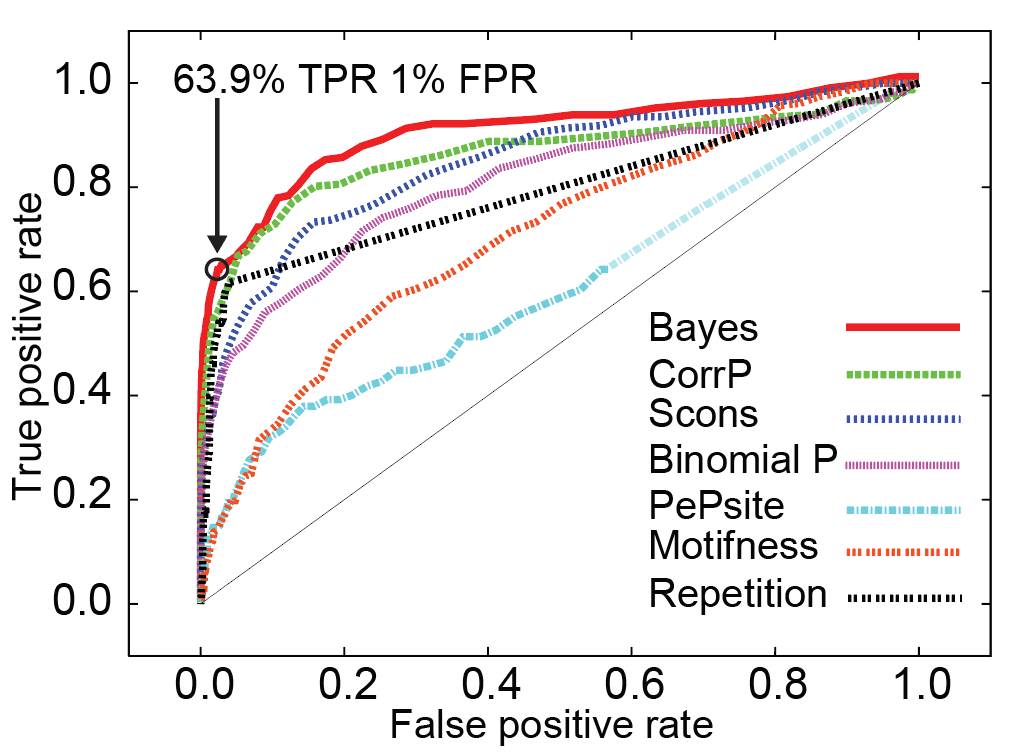
To merge the various metrics above into a single ranking metric, we used naive Bayesian integration as described here. Briefly, the performance of each metric by itself was assessed using a benchmark derived from the ELM database and the true- and false-positive rates used to create the combined metric, which itself has the best overall performance (ROC curve below). Note that both the Bayesian combined metric and our improved P-value (CorrP) also outpreform our original value (Scons). This suggests that both our new P-value and the combination of these weaker predictors (e.g. Motifness,PepSite) leads to a better overall set of motifs.
Publications about these tools
We hope the pipeline will be published soon. For the original DiLiMot (over-representation) method see Neduval et al, 2005. Additional details of the method and the original server can be found in Neduva & Russell, 2006. For the original PepSite reference see Petsalaki et al, 2009. More details are given in the paper on the improvements we made in Trabuco et al, 2012.
